
이제까지의 공부를 통해, 데이터를 수치화해 수학적 / 통계적으로 해석함으로써 각 신경망 유닛이 데이터에 부합하는 최적의 식을 찾는 것이 기계학습의 전반적인 원리임을 알아보았다. 이전글에서는 이 식을 간단하게 H(x)=Wx+b와 같이 기본적인 1차함수로만 다루면서 공부하였지만, [AI-04]에서 공부한 내용에서처럼 신경망은 여러 개의 입력값과 복잡한 노드로 연결되기 때문에 이렇게 간단한 식으로 해결되지는 않는다. 예를 들어, 3개의 입력을 처리하는 신경망 노드의 경우, 아래와 같은 식이 필요할 것이다.
W₁x₁+W₂x₂+W₃x₃-θ
즉, 3개의 각각의 입력값에 대해 서로 다른 가중치를 적용한 값이 각 노드의 편향(임계값, θ)보다 높은지 낮은지에 따라 신경망이 1 (반응) 또는 0 (미반응)으로 다음 노드에 답을 보내면, 다음 노드가 그 값들을 다시 받아 반응하는 식으로 정보의 전달이 이뤄지게 된다.
각 노드는 입력된 값의 계산 결과가 자신의 임계치보다 높은 값인지 낮은 값인지에 따라 0과 1의 두 가지로 반응하게 되는 것인데, 이러한 함수를 계단 함수(Step Function)라고 한다. 인간의 신경을 이루는 뉴런이 정보를 전달할 때 반응을 한다/하지 않는다로 나눠지고 수많은 뉴런의 정보가 종합되어 복잡한 정보가 처리되는데, 인공 신경망 역시 이러한 비슷한 매커니즘을 따르는 것이다.
그런데 이 계단 함수는 그대로 쓰이기에는 적합하지 않은 면이 있는데, 불연속적이고 값이 끊어지는 구간이 있기 때문이다.

위의 그래프가 계단 함수의 그래프인데, u(0)인 지점에서 그래프가 단절됨을 확인할 수 있다. 이는 우리가 인지적으로는 어떤 의미인지 쉽게 파악할 수 있지만 수학적 / 프로그래밍적으로는 처리하기에 애매한 계산 불가 영역을 만들게 된다.
따라서 위의 그래프와 동일한 값을 출력하면서도 연속적인 형태를 사용해야 결과값이 일정한 경향성(Vector)을 가져 수학적/프로그래밍적으로 튀는 구간이 없는 단일 식으로 부호화(Coding)가 가능한 형태가 되는데, 이러한 함수가 바로 시그모이드(Sigmoid) 함수이다.
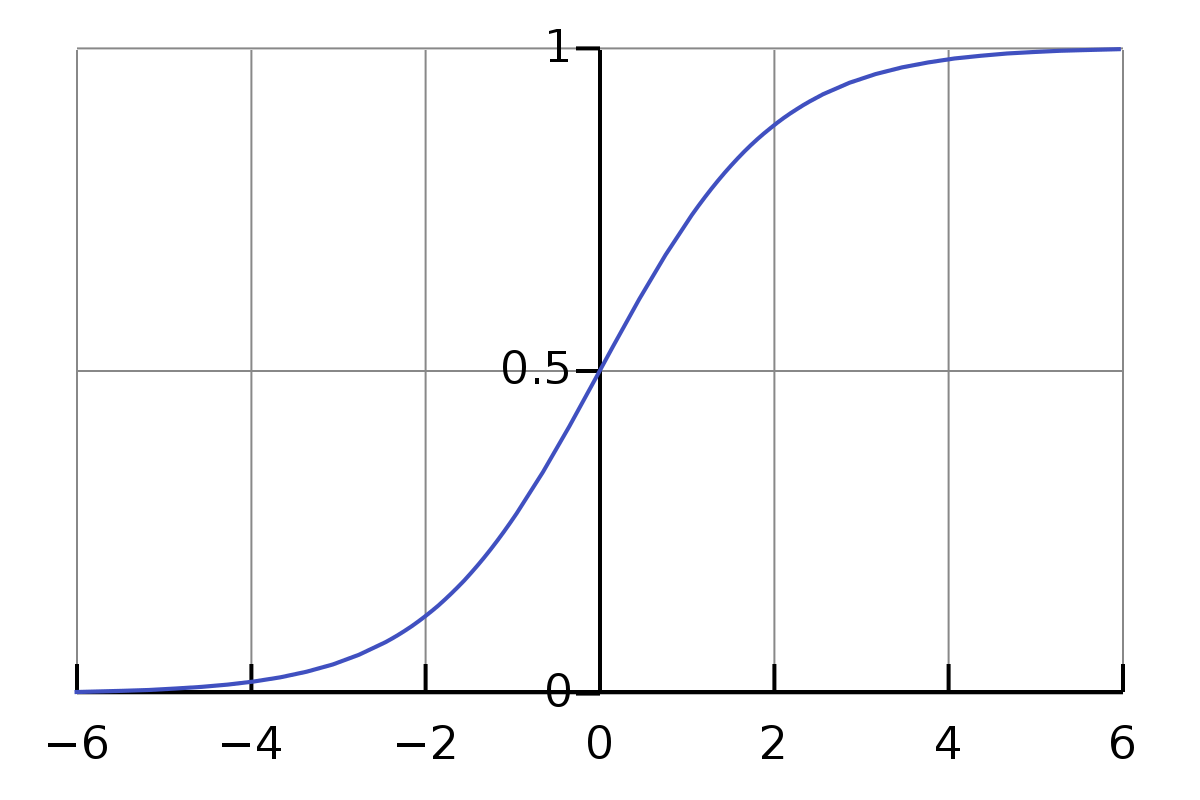
즉, 위의 그래프와 같이 연속성을 갖는 형태의 비선형 함수로 변경함으로써 여러 가지 이점을 가질 수 있는데, 우선 출력값을 1과 0으로 가지면서도 어느 지점에서나 미분하여 기울기를 구할 수 있기 때문에 경사하강법과 같은 최적화 알고리즘을 사용하여 최적의 가중치 값을 찾는 작업이 용이해진다. ([AI-03] 참고)
다시 정리하면 인공 신경망의 각 뉴런은 가중치와 편향(임계값)에 따라 입력 데이터에 대해 0(미반응)과 1(반응)의 결과를 출력하는데, 이를 계단 함수를 통해 표현할 경우 선형 함수의 한계로 인해 미분된 기울기 값이 0으로 동일해지는 문제로 최적화 알고리즘 사용이 어려워지는 문제가 발생하는데, 이를 계단함수를 비선형적으로 변형한 시그모이드 함수로 변형하면 0과 1의 결과를 내는 동일한 처리가 가능하면서도 기울기를 통해 입력값에 따른 비용과 오차를 계산할 수 있어 최적화 알고리즘 사용에 유리해지는 장점이 있다. 결국, 알고리즘(프로그램)에게 신경망의 작업을 할 수 있도록 하면서도 최적화 방법을 명료하게 설명할 수 있는 단순한 방법이라는 의미이다.
'Artificial.Intelligence' 카테고리의 다른 글
| [AI-08] 진흙 속에서 진주 찾기 : KDD (1) | 2024.07.13 |
|---|---|
| [AI-07] 어떻게 학습시킬까? : 레이블과 강화 (3) | 2024.06.16 |
| [AI-05] 수치화하여 방향성 찾기: 벡터와 텐서 (0) | 2024.05.12 |
| [AI-04] 학습이 일어나는 곳 : 인공신경망 (1) | 2024.05.11 |
| [AI-03] 오차를 줄여나가다: 경사하강법 (0) | 2024.05.03 |